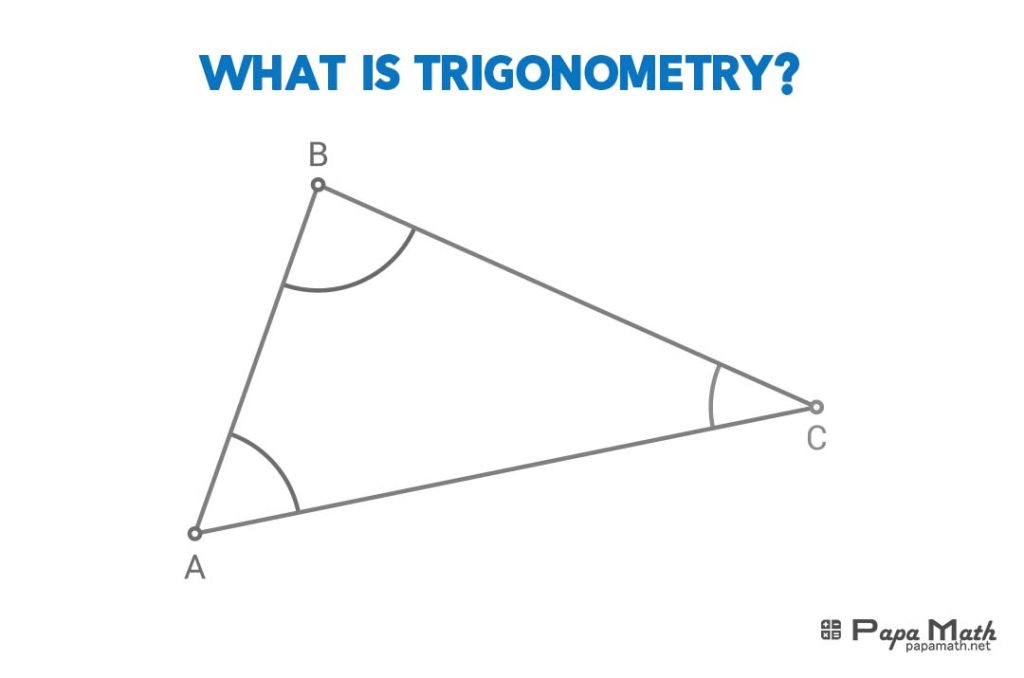
Trigonometry was developed independently by various civilizations, including the ancient Greeks, Egyptians, and Babylonians. The branch of mathematics that deals with relationships between the sides and angles of triangles is trigonometry. The concept of trigonometry is given by the Greek mathematician Hipparchus. Here we learn about the various identities and formulas of trigonometry and the real-life examples or applications of trigonometry.
Trigonometric Functions
Trigonometric functions are mathematical functions that relate the angles of a right triangle to the lengths of its sides. They are fundamental in trigonometry, the branch of mathematics concerned with the relationships between angles and the lengths of the sides of triangles.
What are the six basic Trigonometric Functions?
There are \(6\) trigonometric function are
$$\text{sine function}$$
$$\text{cosine function}$$
$$\text{tangent function}$$
$$\text{Secant function}$$
$$\text{Cosecant function}$$
$$\text{Cotangent function}$$
What is the Sine Function in Trigonometry?
The sine of an acute angle in a right triangle is the ratio of the side opposite of the angle to the hypotenuse.
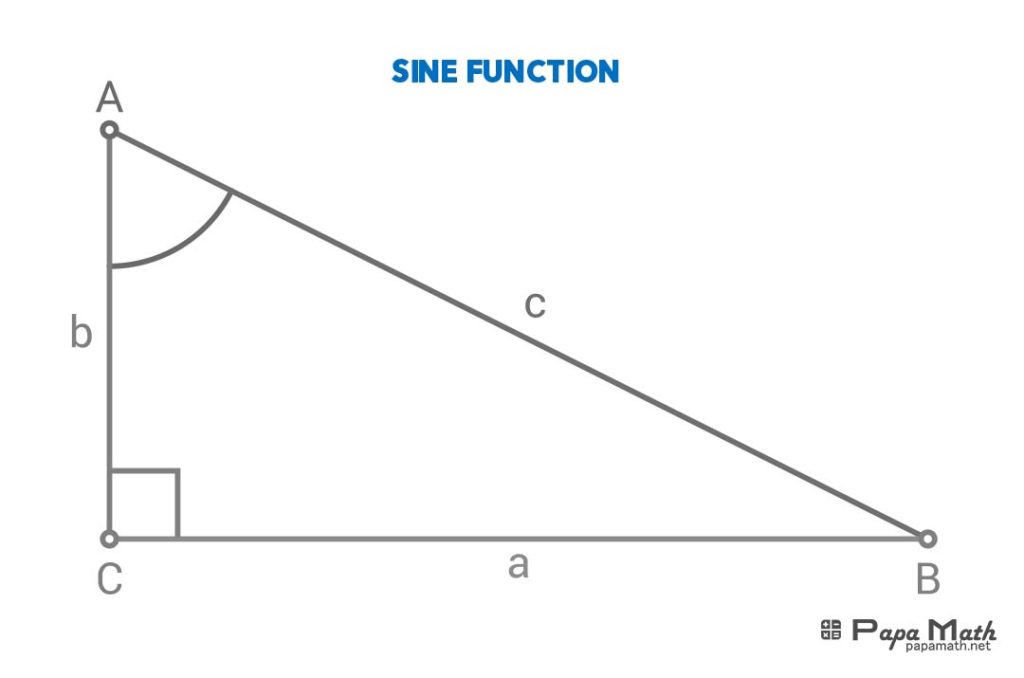
In a right triangle \(\triangle{ABC}\), sine of \(\angle{A}\) is given by
$$\sin{(\angle{A})}=\frac{a}{c}$$
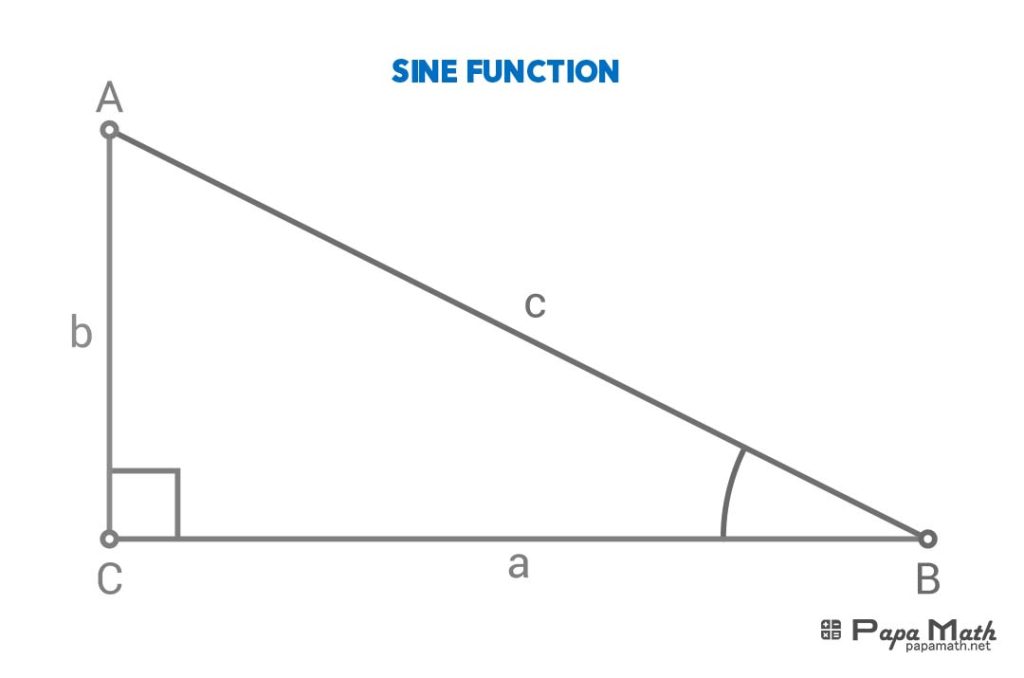
In a right triangle \(\triangle{ABC}\), sine of \(\angle{B}\) is given by
$$\sin{(\angle{B})}=\frac{b}{c}$$
What is the Cosine Function in Trigonometry?
The cosine of an acute angle in a right triangle is the ratio of the side adjacent to the angle to the hypotenuse.
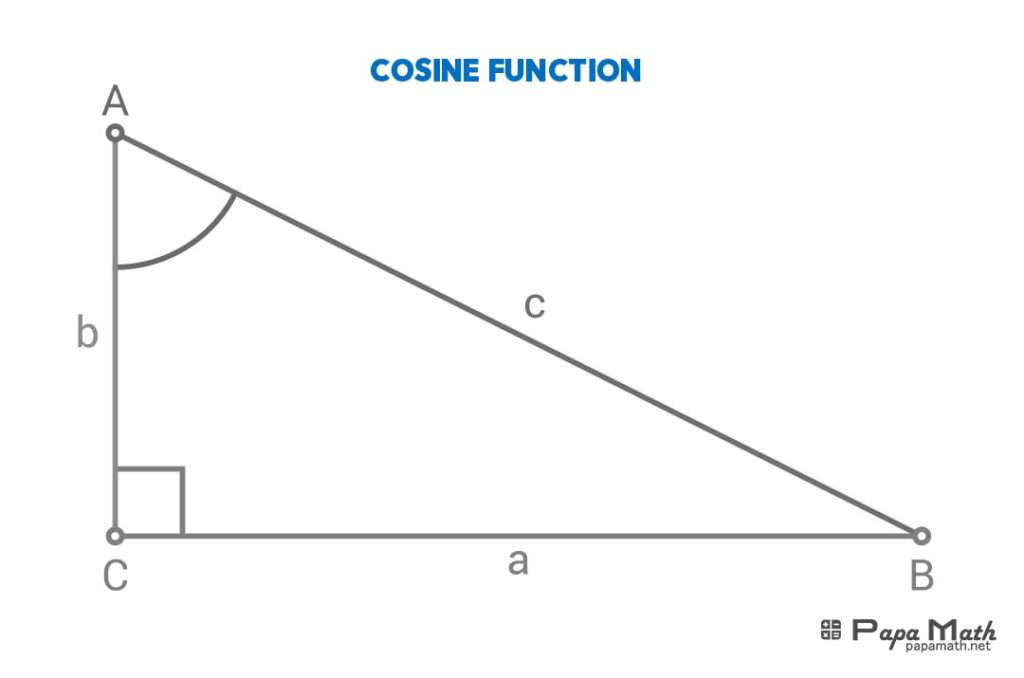
In a right triangle \(\triangle{ABC}\), cosine of \(\angle{A}\) is given by
$$\cos{(\angle{A})}=\frac{b}{c}$$
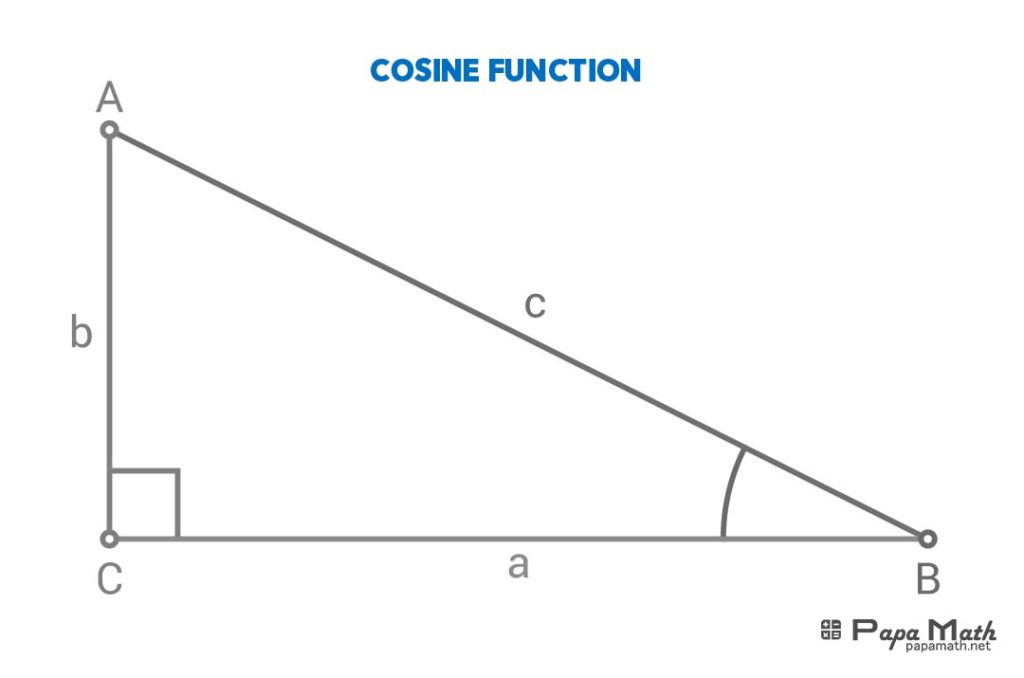
In a right triangle \(\triangle{ABC}\), cosine of \(\angle{B}\) is given by
$$\cos{(\angle{B})}=\frac{a}{c}$$
What is the Tangent Function in Trigonometry?
The tangent of an acute angle in a right triangle is the ratio of the side opposite of the angle to the side adjacent to the angle.
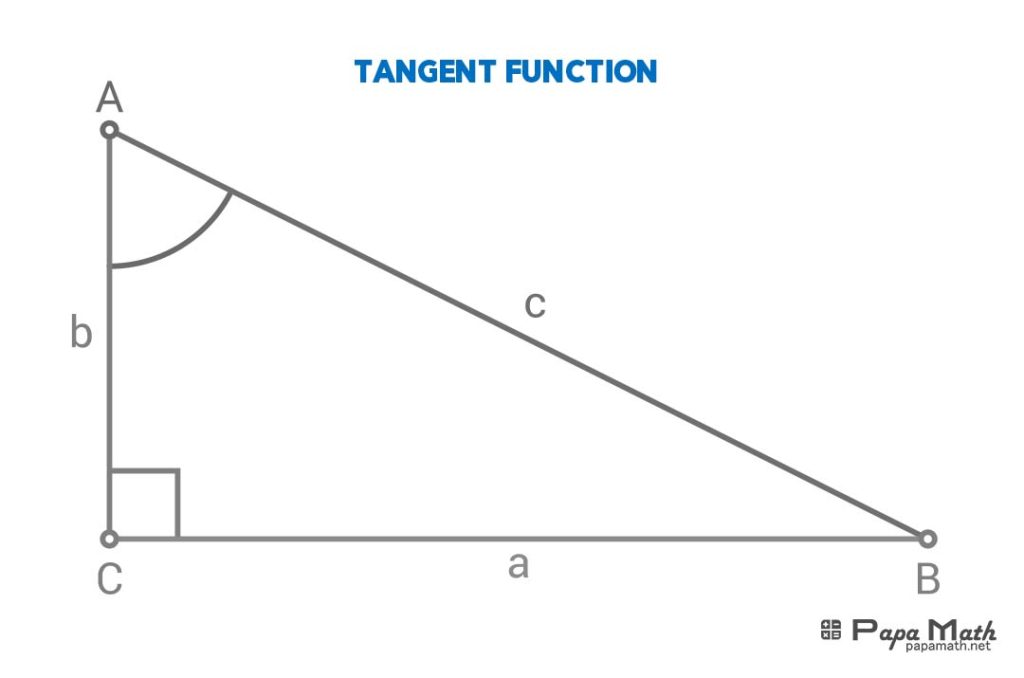
In a right triangle \(\triangle{ABC}\), tangent of \(\angle{A}\) is given by
$$\tan{(\angle{A})}=\frac{a}{b}$$
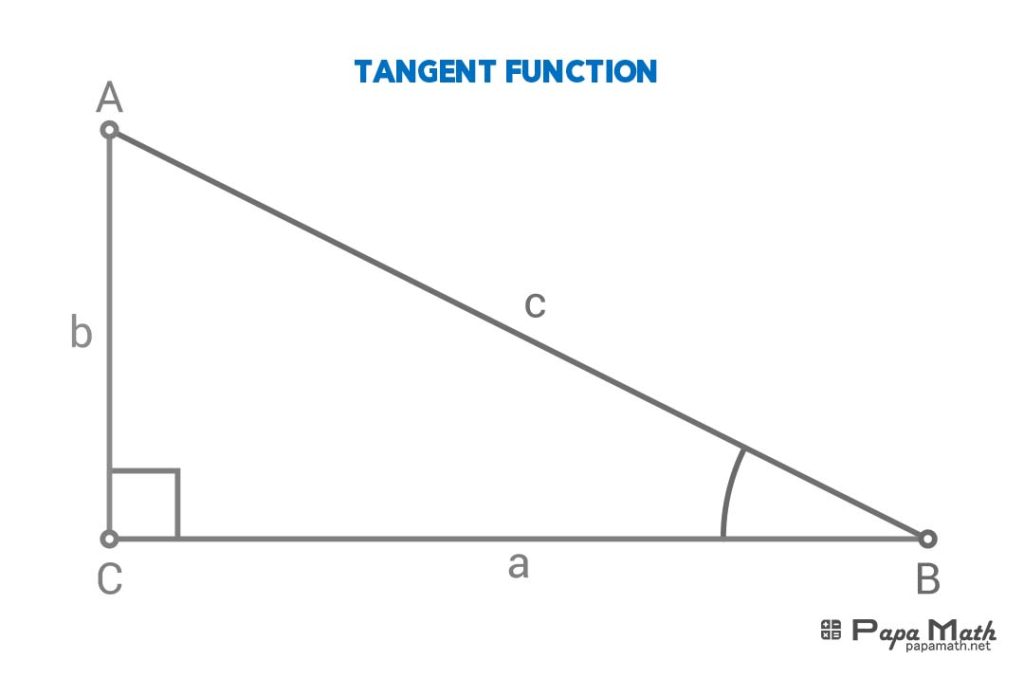
In a right triangle \(\triangle{ABC}\), tangent of \(\angle{B}\) is given by
$$\tan{(\angle{B})}=\frac{b}{a}$$
What is the Cosecant Function in Trigonometry?
The cosecant of an acute angle in a right triangle is the ratio of the hypotenuse to the side opposite of the angle.
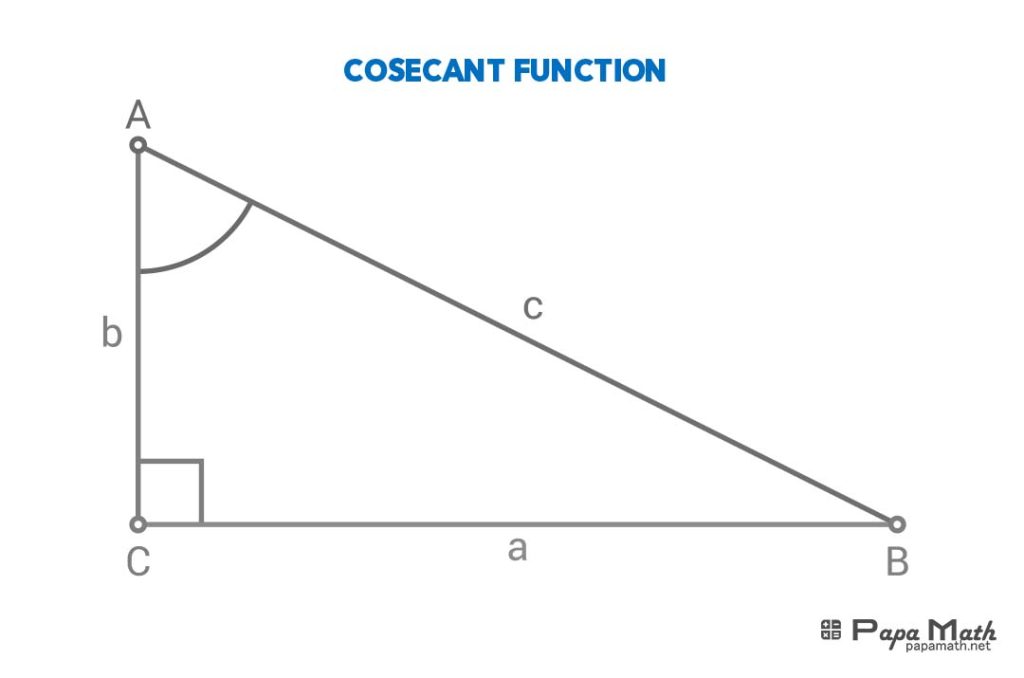
In a right triangle \(\triangle{ABC}\), cosecant of \(\angle{A}\) is given by
$$\csc{(\angle{A})}=\frac{c}{a}$$
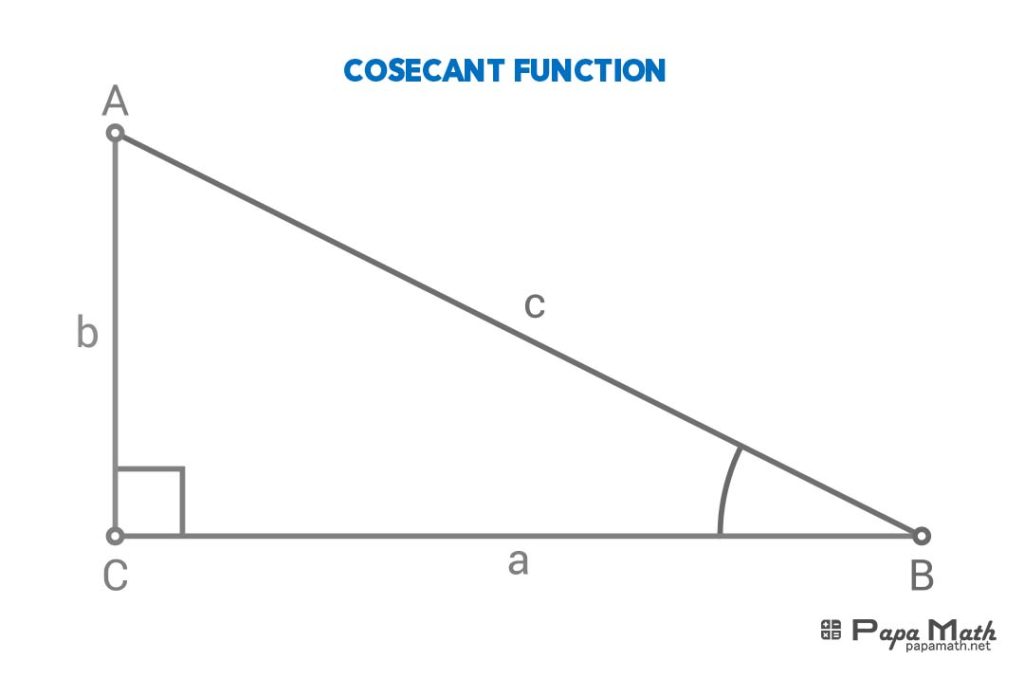
In a right triangle \(\triangle{ABC}\), cosecant of \(\angle{B}\) is given by
$$\csc{(\angle{B})}=\frac{c}{b}$$
What is the Cotangent Function in Trigonometry?
The cotangent of an acute angle in a right triangle is the ratio of the side adjacent to the angle to the side opposite of the angle.
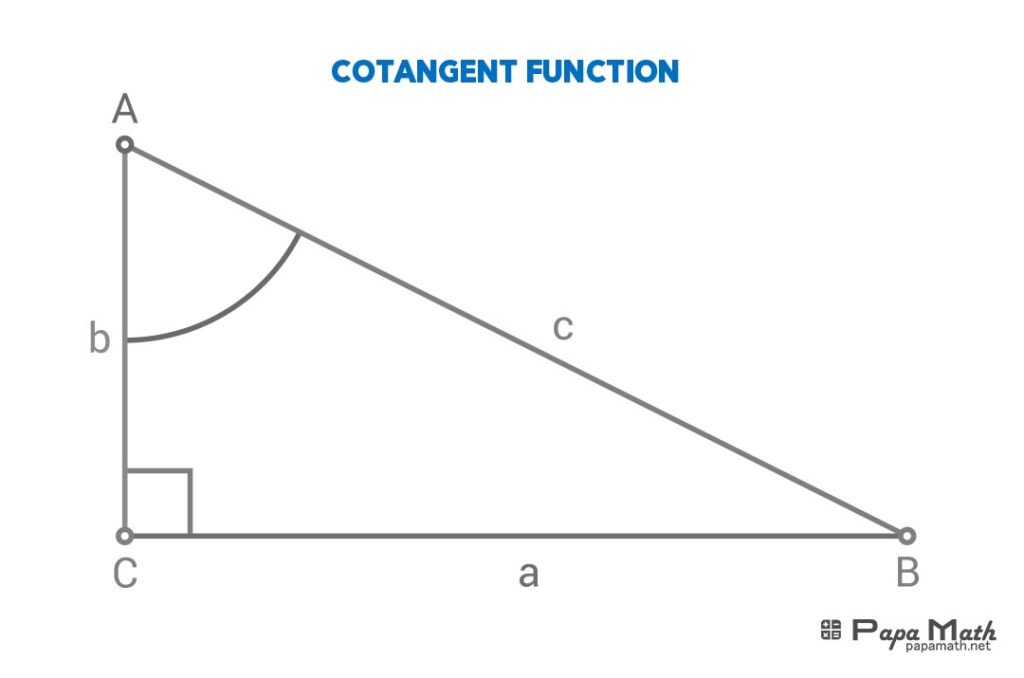
In a right triangle \(\triangle{ABC}\), cotangent of \(\angle{A}\) is given by
$$\cot{(\angle{A})}=\frac{b}{a}$$
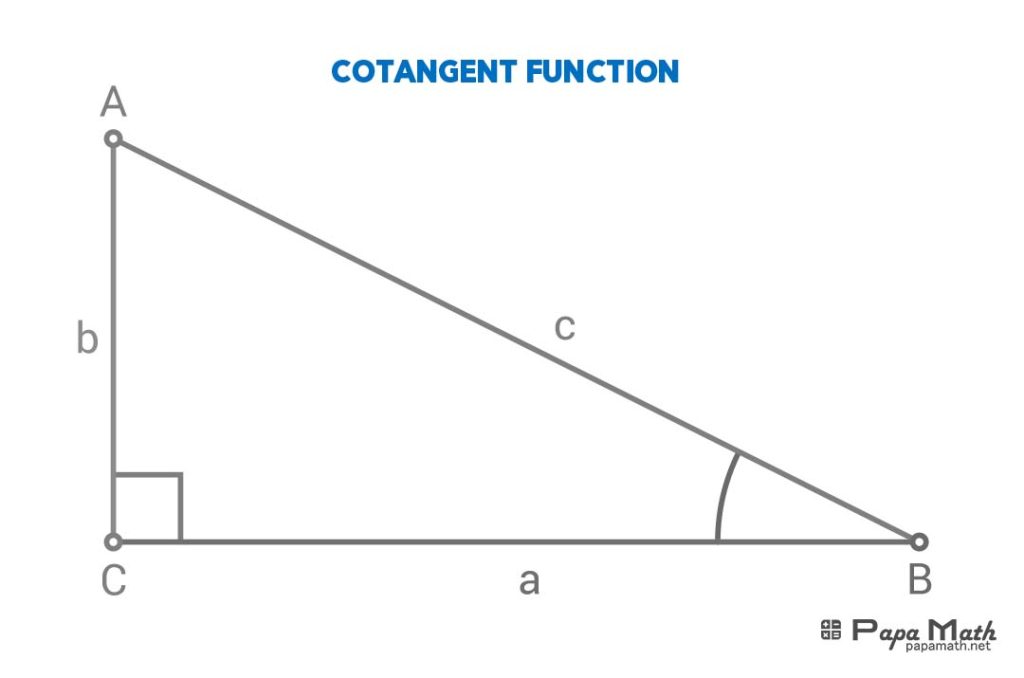
In a right triangle \(\triangle{ABC}\), cotangent of \(\angle{B}\) is given by
$$\cot{(\angle{B})}=\frac{a}{b}$$
What is the Secant Function in Trigonometry?
The secant of an acute angle in a right triangle is the ratio of the hypotenuse to the side adjacent to the angle.
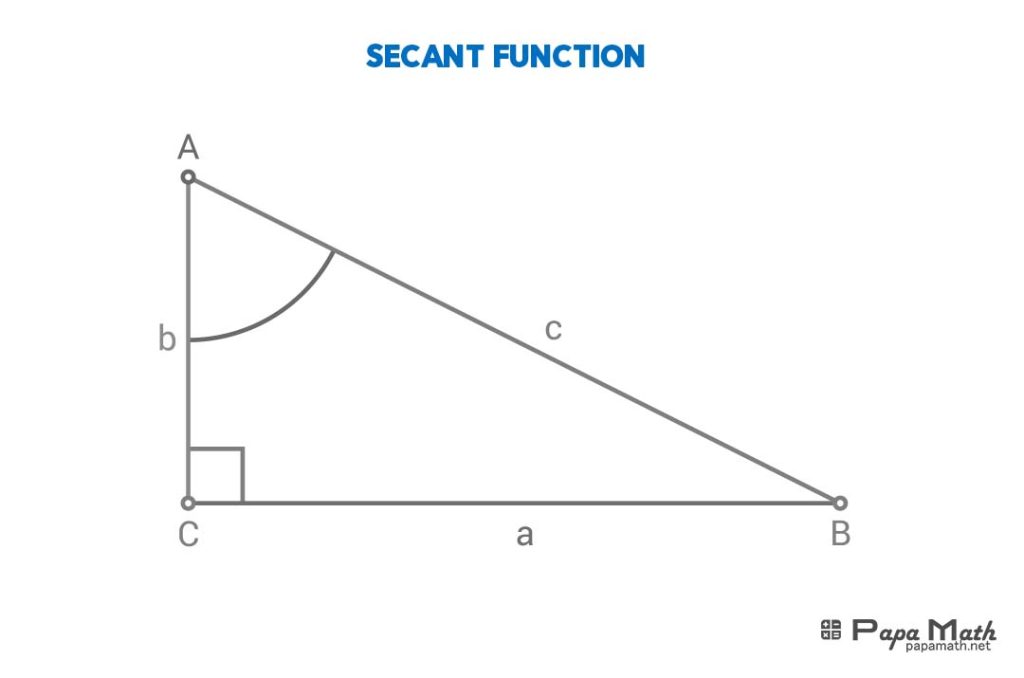
In a right triangle \(\triangle{ABC}\), secant of \(\angle{A}\) is given by
$$\sec{(\angle{A})}=\frac{c}{b}$$
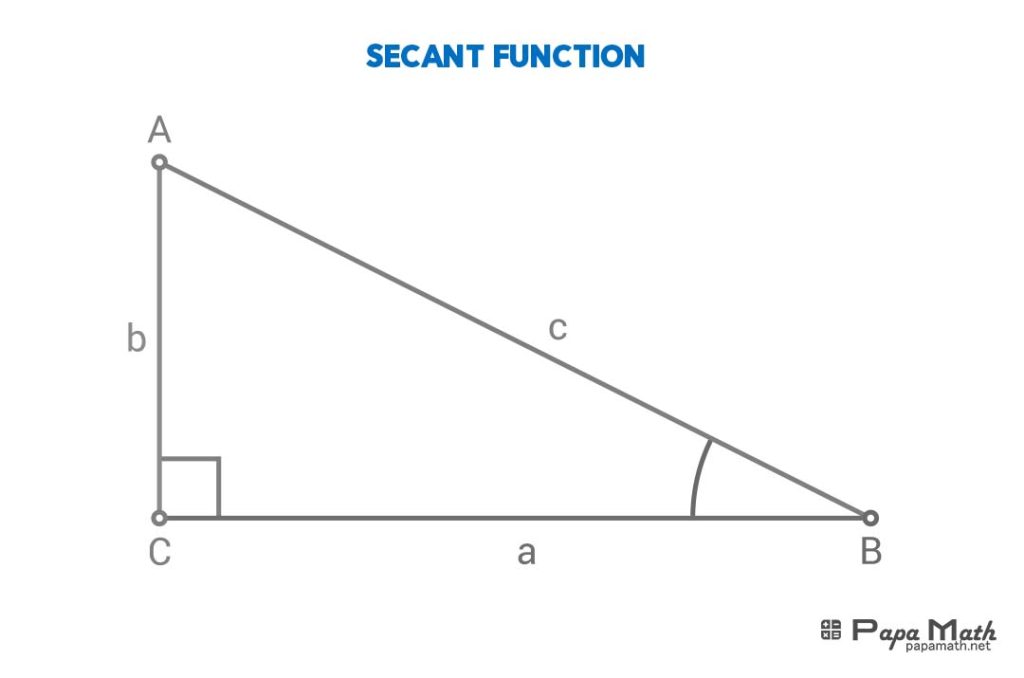
In a right triangle \(\triangle{ABC}\), secant of \(\angle{B}\) is given by
$$\sec{(\angle{B})}=\frac{c}{a}$$
Trigonometry Identities
Trigonometric identities are equations involving trigonometric functions that are true for all values of the variables. Some of the important identities include:
Pythagorean Identities
$$\sin^{2}{(\theta)}+\cos^{2}{(\theta)}=1$$
$$1+\tan^{2}{(\theta)}=\sec^{2}{(\theta)}$$
$$1+\cot^{2}{(\theta)}=\csc^{2}{(\theta)}$$
Trigonometry Formulas
Trigonometry is filled with formulas that help us solve problems involving triangles. These formulas include
Double Angle Identities in Trigonometry
Double angle identities are formulas that express trigonometric functions of double angles in terms of trigonometric functions of the original angles. These identities are useful for simplifying trigonometric expressions.
$$\sin{(2\theta)}=2\sin{(\theta)}\cos{(\theta)}$$
$$\cos{(2\theta)}=\cos^{2}{(\theta)}-\sin^{2}{(\theta)}$$
$$\tan{(2\theta)}=\frac{2\tan{(\theta)}}{1-\tan^{2}{(\theta)}}$$
$$\cot{(2\theta)}=\frac{\cot^{2}{(\theta)}-1}{2\cot{(\theta)}}$$
Sum and Difference Identities
For angles \({\alpha}\) and \({\beta}\), we have the following relationships
$$\sin{(\alpha\pm\beta)}=\sin{(\alpha)}\cos{(\beta)}\pm\cos{(\alpha)}\sin{(\beta)}$$
$$\cos{(\alpha\pm\beta)}=\cos{(\alpha)}\cos{(\beta)}\mp\sin{(\alpha)}\sin{(\beta)}$$
$$\tan{(\alpha\pm\beta)}=\frac{\tan{(\alpha)}\pm\tan{(\beta)}}{1\mp\tan{(\alpha)}\tan{(\beta)}}$$
Sine and Cosine Laws
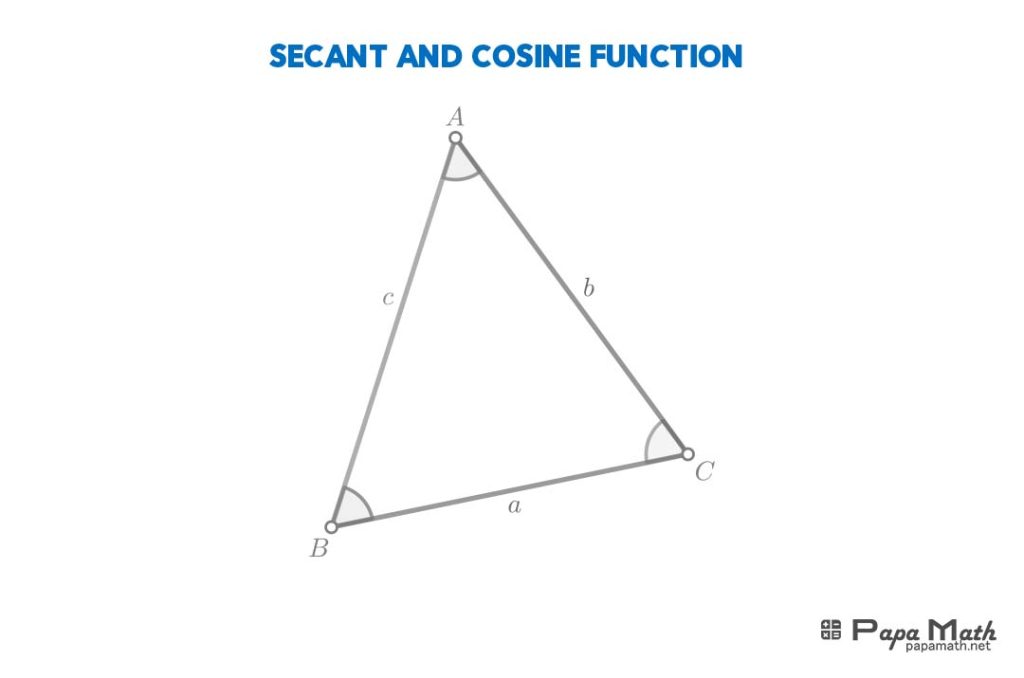
If \(A\), \(B\) and \(C\) are angles and \(a\), \(b\) and \(c\) are the sides of a triangle, then,
Sine Law
$$\frac{\sin{(A)}}{a}=\frac{\sin{(B)}}{b}=\frac{\sin{(C)}}{c}$$
Cosine Law
$$a^{2}=b^{2}+c^{2}-2bc\cos{(A)}$$
$$b^{2}=a^{2}+c^{2}-2ac\cos{(B)}$$
$$c^{2}=a^{2}+b^{2}-2ab\cos{(C)}$$
Trigonometry Table
A trigonometry table provides a set of pre-calculated values for trigonometric functions such as sine, cosine, and tangent for different angles. These tables were commonly used before the advent of calculators to facilitate trigonometric calculations.
| Angle \(({\circ})\) | Sine \(({\sin})\) | Cosine \(({\cos})\) | Tangent \(({\tan})\) | Cosecant \(({\csc})\) | Secant \(({\sec})\) | Cotangent \(({\cot})\) |
| \(0\) | \(0\) | \(1\) | \(0\) | \(\infty \) | \(0\) | \(\infty \) |
| \(30\) | \(\frac12\) | \(\frac{\sqrt{3}}{2}\) | \(\frac{\sqrt{3}}{3}\) | \(2\) | \(\frac{2}{\sqrt{3}}\) | \(\sqrt{3}\) |
| \(45\) | \(\frac{\sqrt{2}}{2}\) | \(\frac{\sqrt{2}}{2}\) | \(1\) | \(\sqrt{2}\) | \(\sqrt{2}\) | \(1\) |
| \(60\) | \(\frac{\sqrt{3}}{2}\) | \(\frac12\) | \(\sqrt{3}\) | \(\frac{2}{\sqrt{3}}\) | \(2\) | \(\frac{\sqrt{3}}{3}\) |
| \(90\) | \(1\) | \(0\) | \(\infty \) | \(\infty \) | \(\infty \) | \(0\) |
Unit Circle Trigonometry
The unit circle is a circle with a radius of 1 unit, centred at the origin of a Cartesian coordinate system. Unit circle trigonometry involves defining trigonometric functions using the coordinates of points on the unit circle.
Rules in Trigonometry
Trigonometry has several rules governing the manipulation and calculation of trigonometric expressions. These rules include addition and subtraction formulas, as well as various properties of trigonometric functions that are given above.
Circles and Trigonometry
Trigonometry also finds applications in studying circles, especially in geometry. The relationships between the angles and arcs of circles can be analysed using trigonometric concepts.
Inverse Functions in Trigonometry
Inverse trigonometric functions are used to find the angle associated with a given trigonometric ratio. They provide a way to determine angles from known side lengths in a right triangle.
There are six inverse functions in trigonometry, which are
$$\sin^{-1}{(x)}$$
$$\cos^{-1}{(x)}$$
$$\tan^{-1}{(x)}$$
$$\csc^{-1}{(x)}$$
$$\sec^{-1}{(x)}$$
$$\cot^{-1}{(x)}$$
Even and Odd Trigonometric Functions
Trigonometric functions can be classified as even or odd based on their symmetry properties. Even functions exhibit symmetry about the y-axis, while odd functions exhibit symmetry about the origin.
The mathematical form of the even function is:
$$f(-x)=f(x)$$
The even trigonometric functions are:
$$\cos{(-x)}=\cos{(x)}$$
$$\sec{(-x)}=\sec{(x)}$$
The mathematical form of the odd function is:
$$f(-x)=-f(x)$$
The odd trigonometric functions are:
$$\sin{(-x)}=-\sin{(x)}$$
$$\sec{(-x)}=-\sec{(x)}$$
$$\tan{(-x)}=-\tan{(x)}$$
$$\cot{(-x)}=-\cot{(x)}$$
“If you want to delve deeper into the concept of Trigonometry, click here to read more.”
FAQs
Is Trigonometry Hard?
Trigonometry can be challenging for some people, but with practice, it becomes more manageable.
Is Algebra and Trigonometry the same?
Algebra and Trigonometry are related but not the same; trigonometry deals specifically with angles and their relationships.
Angle Symbol in Trigonometry?
The angle symbol used in trigonometry is typically represented by the Greek letter theta /(/theta/)
Six functions of trigonometry?
The six trigonometric functions are sine, cosine, tangent, cosecant, secant, and cotangent.
Who invented trigonometry?
Trigonometry was developed independently by various civilizations, including the ancient Greeks, Egyptians, and Babylonians.
Conclusion
Trigonometry is a vital branch of mathematics that explores the relationships between angles and the sides of triangles. Developed independently by ancient civilizations like the Greeks, Egyptians, and Babylonians, it introduces six fundamental trigonometric functions: sine, cosine, tangent, cosecant, secant, and cotangent. These functions help us solve various geometric problems, especially those involving right triangles.
In addition to these functions, trigonometry involves many identities, formulas, and laws such as the Pythagorean identities, double angle identities, and sine, and cosine laws. These tools are essential for simplifying expressions, calculating unknown angles or sides in triangles, and understanding the properties of trigonometric functions.
Trigonometry also finds applications in real-life scenarios like physics, engineering, astronomy, and more. While it can be challenging initially, consistent practice and understanding of its concepts lead to mastery and proficiency in solving trigonometric problems effectively.
“Please feel free to ask your query, and I’ll be happy to answer your query.“