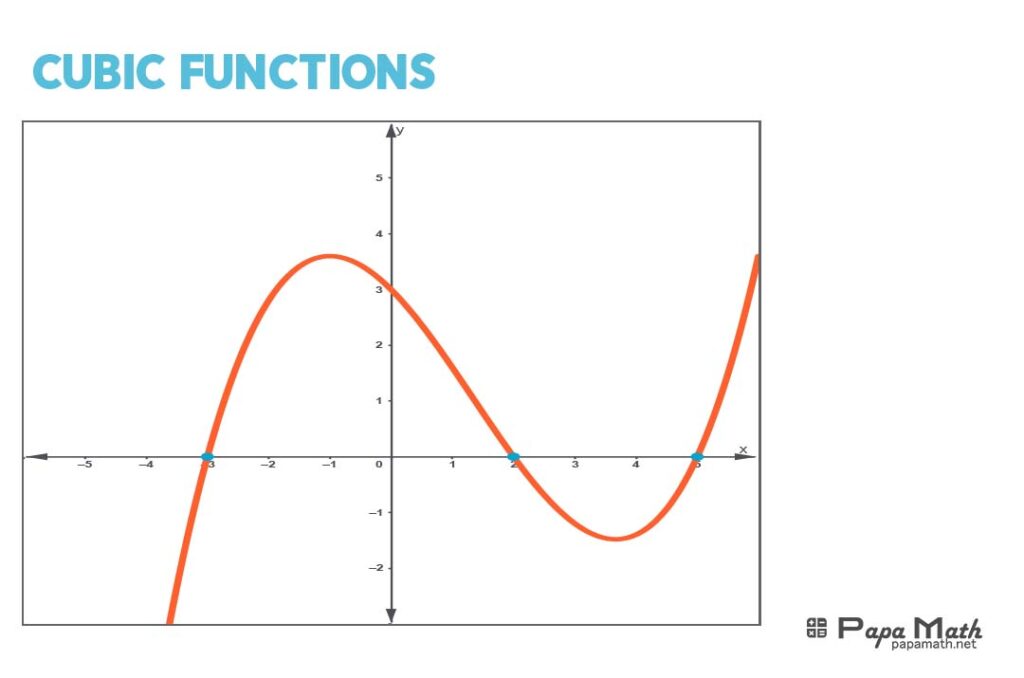
Cubic functions are a fundamental concept in algebra and mathematics, representing a polynomial equation of degree three. The general form of a cubic function is \(ax^3 + bx^2 + cx + d\), where \(a\), \(b\), \(c\), and \(d\) are constants and \(x\) is the variable. Cubic functions have various applications in physics, engineering, economics, and computer science, modeling real-world phenomena like motion, growth, and optimization. Understanding cubic functions and their graphs is crucial for problem-solving and critical thinking in these fields. In this article, we will delve into the properties, behavior, and applications of cubic functions, exploring their graphs, zeros, factorization, and transformations.
Finding the Zeros of a Cubic Function
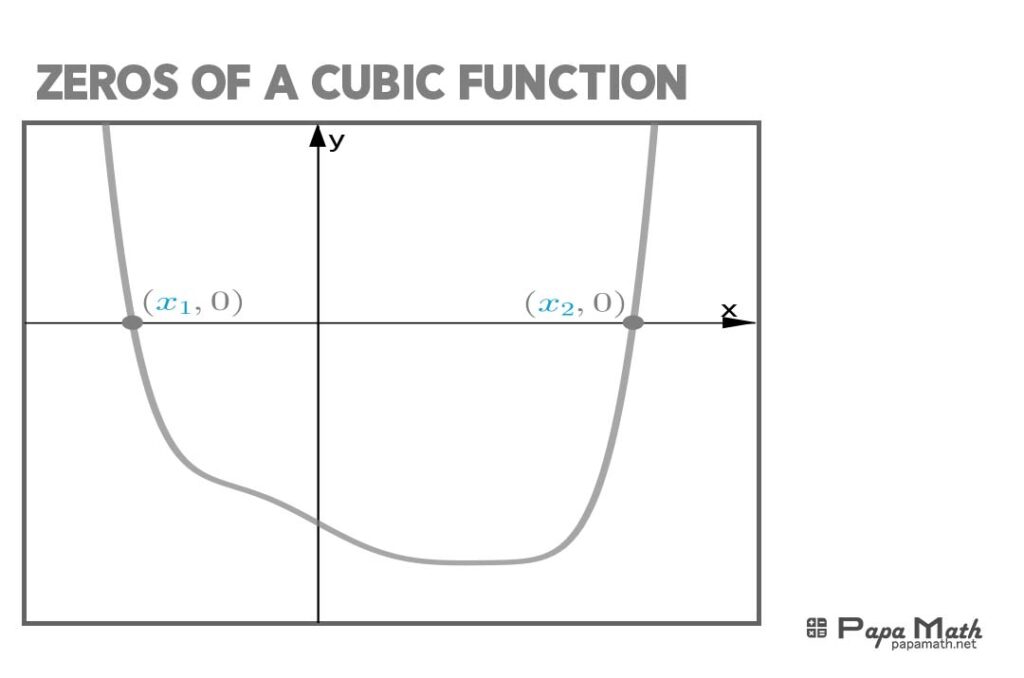
Finding the zeros of a cubic function is essential for understanding its behavior and graph. The zeros of a cubic function are the solutions to the equation \(f(x) = 0\). There are various methods to find the zeros, including factoring, synthetic division, and numerical methods. Factoring is the most efficient method when possible, as it provides exact solutions. Synthetic division is used when factoring is not feasible, and numerical methods like the Rational Root Theorem and approximation techniques are employed when exact solutions are difficult to obtain. Understanding the zeros of a cubic function is vital for analyzing its graph, identifying maxima and minima, and applying the function to real-world problems.
Factoring Cubic Functions
Factoring cubic functions is a crucial skill in algebra and mathematics, enabling us to simplify expressions, solve equations, and graph functions. Factoring cubic functions involves expressing the function as a product of lower-degree polynomials. There are various methods for factoring cubic functions, including factoring out the greatest common factor (GCF), grouping, and the AC method. Factoring cubic functions is essential for finding the zeros, expanding the function, and identifying the graph’s critical points. Mastering factoring techniques is vital for success in mathematics and problem-solving.
Expanding Cubic Functions
Expanding cubic functions is the process of expressing the function in its simplest form, revealing its underlying structure. Expansion involves multiplying the factors of the function, using techniques like the binomial theorem and polynomial long division. Expanding cubic functions is crucial for identifying the function’s behavior, finding the zeros, and graphing the function. Understanding the expansion of cubic functions is vital for applications in physics, engineering, and computer science, where modeling and problem-solving rely on the manipulation of polynomial equations.
Domain and Range of Cubic Functions
The domain and range of a cubic function are essential concepts in understanding its behavior and graph. The domain refers to the set of input values \(x\) for which the function is defined, while the range is the set of output values \(y\) that the function can take. Cubic functions have a domain of all real numbers, as they are defined for all values of \(x\). The range of a cubic function depends on the function’s shape and orientation, which can be determined by analyzing the function’s graph. Understanding the domain and range is vital for applying cubic functions to real-world problems, where input and output values must be considered.
Asymptotes of Cubic Functions
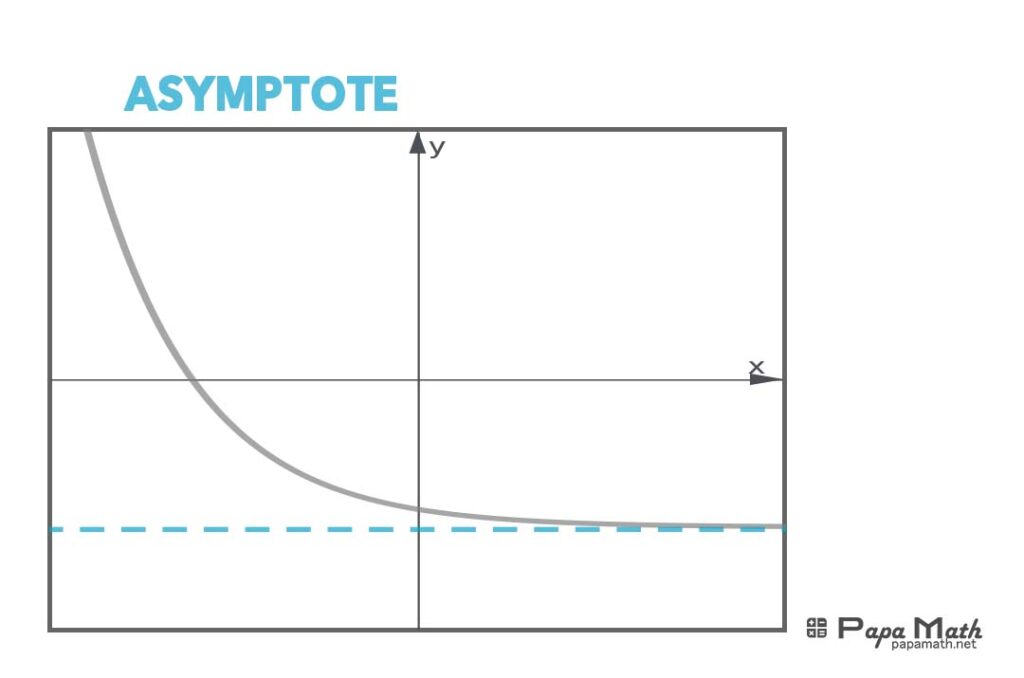
Asymptotes are lines that a function approaches as the input values \(x\) increase or decrease without bound. Cubic functions can have horizontal, vertical, or oblique asymptotes, depending on the function’s shape and orientation. Horizontal asymptotes represent the function’s end behavior, while vertical asymptotes indicate a discontinuity in the function. Oblique asymptotes occur when the function approaches a linear function as x increases or decreases without bound. Identifying asymptotes is crucial for understanding the function’s behavior, graphing the function, and applying the function to real-world problems.
End Behavior of Cubic Functions
The end behavior of a cubic function refers to its behavior as the input values \(x\) increase or decrease without bound. Cubic functions can exhibit various end behaviors, including increasing or decreasing without bound, approaching a horizontal asymptote, or oscillating between positive and negative values. Understanding the end behavior is vital for graphing the function, identifying asymptotes, and applying the function to real-world problems. The end behavior of a cubic function can be determined by analyzing the function’s leading term, which dominates the function’s behavior as \(x\) increases or decreases without bound.
Critical and Inflection Points of Cubic Functions
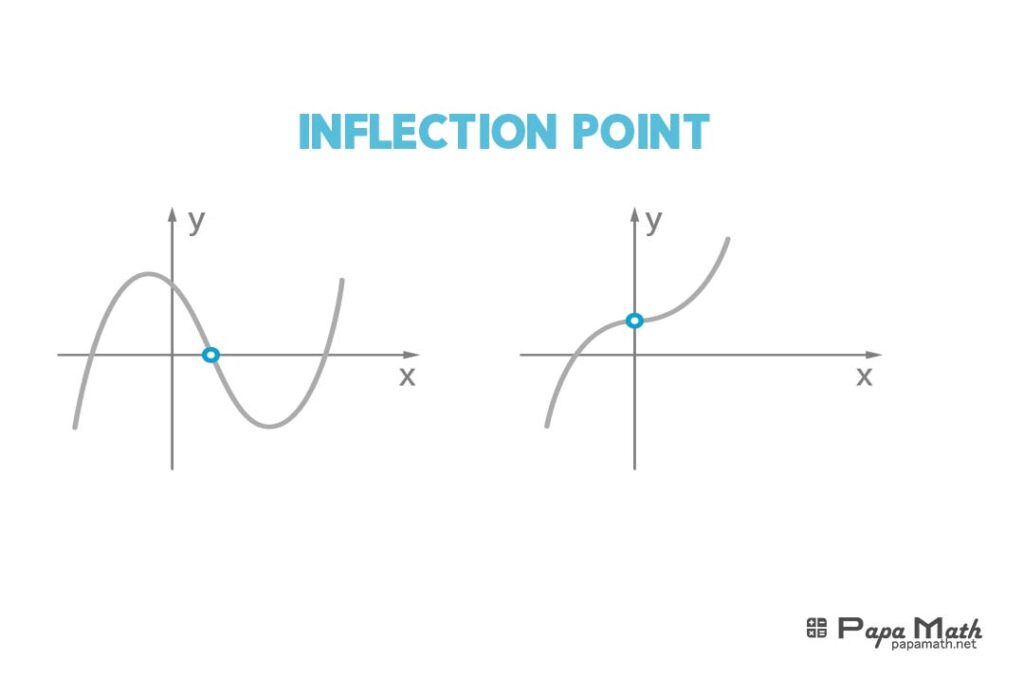
Critical points are values of x where the function’s derivative is equal to zero or undefined. Inflection points are values of \(x\) where the function’s concavity changes. Cubic functions can have various critical and inflection points, depending on the function’s shape and orientation. Identifying critical and inflection points is crucial for understanding the function’s behavior, graphing the function, and applying the function to real-world problems. Critical and inflection points can be determined by analyzing the function’s derivative and second derivative.
Transforming the Graph of a Cubic Function
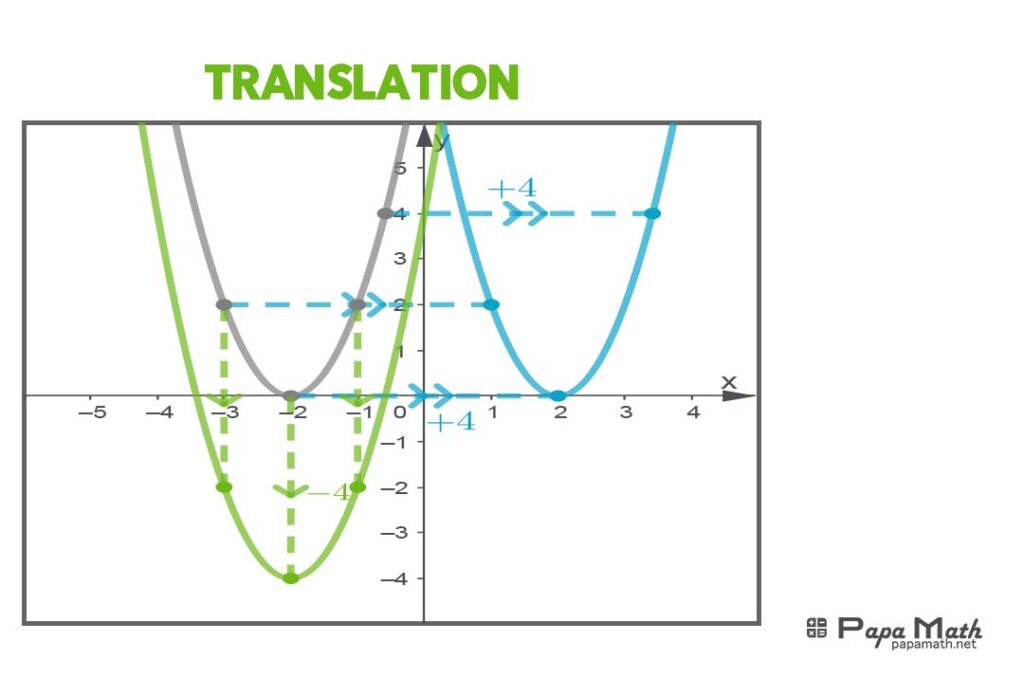
Transforming the graph of a cubic function involves changing its shape, size, and orientation. Various transformations can be applied to cubic functions, including:
| Transformation | Description | Equation Transformation | Graph Effect |
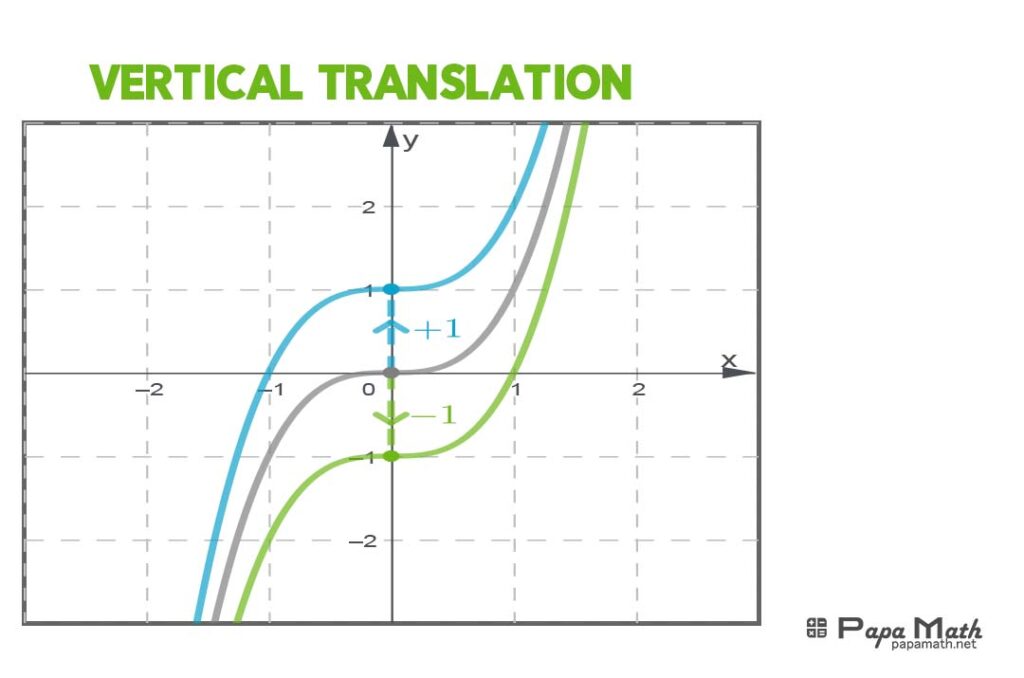
| Vertical Shifts | Moving the graph up or down | \(y = f(x) + k\) | Moves the graph up by k units if \(k > 0\) and down by \(k\) units if \(k < 0\) |
| Horizontal Shifts | Moving the graph left or right | \(y = f(x – h)\) | Moves the graph right by h units if \(h > 0\) and left by \(h\) units if \(h < 0\) |
| Reflections | Flipping the graph over the x-axis or y-axis | \(y = -f(x)\) (x-axis reflection) | Reflects the graph over the x-axis |
| \(y = f(-x)\) (y-axis reflection) | Reflects the graph over the y-axis | ||
| Scaling | Stretching or compressing the graph vertically or horizontally | \(y = c \cdot f(x)\) (vertical scaling) | Stretches the graph vertically by a factor of \(c\) if \(c > 1\); compresses it if \(0 < c < 1\) |
| \(y = f(cx)\) (horizontal scaling) | Compresses the graph horizontally by a factor of \(c\) if \(c > 1\); stretches it if \(0 < c < 1\) |
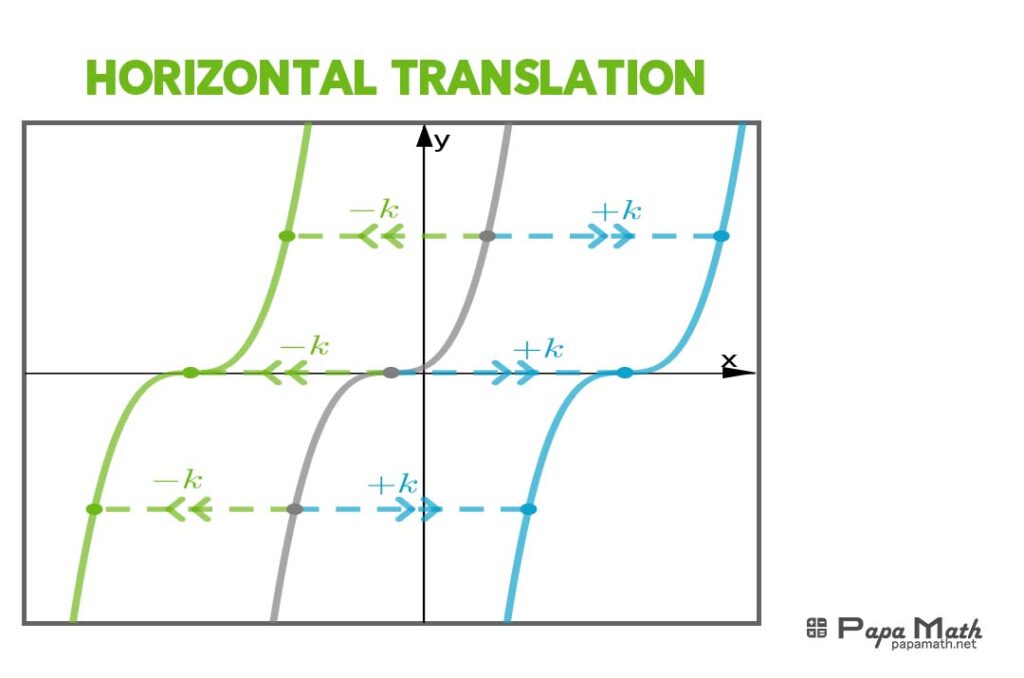
Understanding transformations is vital for graphing cubic functions, identifying asymptotes, and applying the function to real-world problems. Transformations can be applied to cubic functions by modifying the function’s equation, allowing us to visualize and analyze the transformed graph.
Graphing a Cubic Function
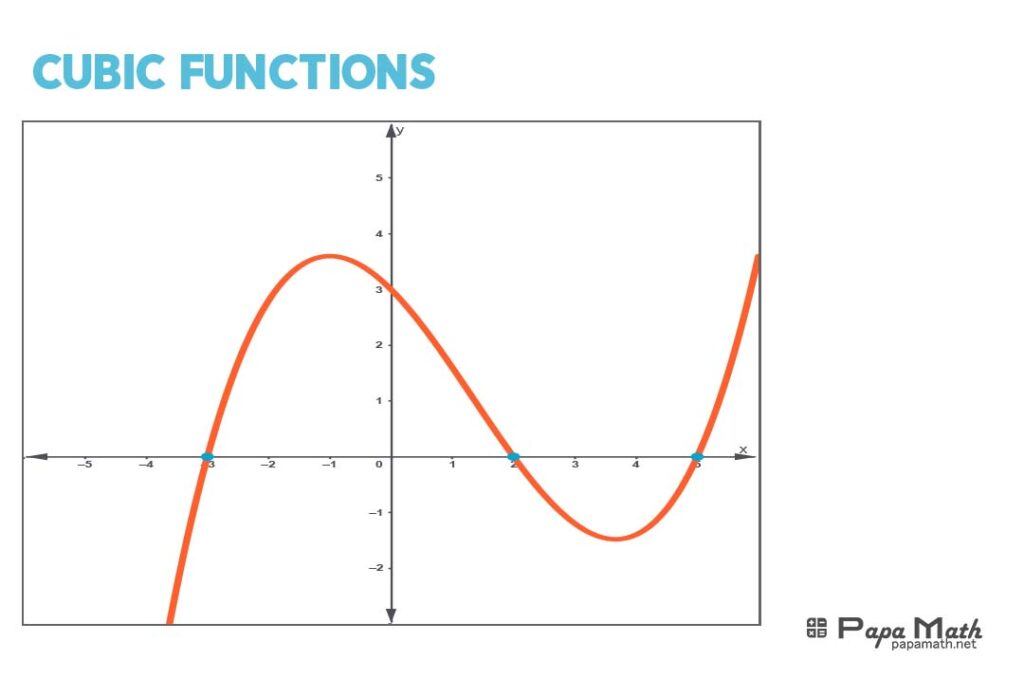
Graphing a cubic function involves visualizing its behavior and shape. The graph of a cubic function can be obtained by plotting points, using a graphing calculator, or applying transformations. Understanding the graph’s shape, orientation, and asymptotes is crucial for analyzing the function’s behavior, identifying critical points, and applying the function to real-world problems. Graphing cubic functions is essential for problem-solving in physics, engineering, economics, and computer science.
The graph of the cubic function \(f(x)=x^{3}-4 x^{2}-11 x+30\)
Table of Values
| \(x\) | \(f(x)\) |
| -3 | -6 |
| -2 | 12 |
| -1 | 24 |
| 0 | 30 |
| 1 | 28 |
| 2 | 12 |
| 3 | -6 |
| 4 | -30 |
| 5 | 0 |
| 6 | 42 |
Table of Zeros
| Zero | Value at Zero (f(x)) |
| 2 | 0 |
| -3 | 0 |
| 5 | 0 |
In the table of values, various \(x\)-values are chosen to show how the function behaves. The table of zeros specifically lists the \(x\)-values at which the function equals zero, indicating the points where the graph intersects the \(x\)-axis.
Applications of Cubic Functions
Cubic functions have various applications in real-world problems, including:
| Field | Applications |
| Physics | Modeling motion, force, and energy |
| Engineering | Designing bridges, buildings, and electronic circuits |
| Economics | Modeling growth, inflation, and supply-demand curves |
| Computer Science | Algorithms for data analysis and machine learning |
Understanding cubic functions and their graphs is vital for problem-solving and critical thinking in these fields. Cubic functions can model complex phenomena, allowing us to analyze and predict behavior, optimize solutions, and make informed decisions.
Let \(p(x)\) be a cubic polynomial whose leading coefficient is \(1\), \(p(1) =1 ,p(2) =2, p(3) =3\), what is value of \(p(4)\)?
Since \(p(x)\) is a cubic polynomial with leading coefficient \(1\), we can write it in the form:
$$p(x) = x^3 + ax^2 + bx + c$$
We are given that \(p(1) = 1\), \(p(2) = 2\), and \(p(3) = 3\). Let’s use this information to find the values of \(a\), \(b\), and \(c\).
$$p(1) = 1^3 + a(1)^2 + b(1) + c = 1 + a + b + c = 1$$
$$p(2) = 2^3 + a(2)^2 + b(2) + c = 8 + 4a + 2b + c = 2$$
$$p(3) = 3^3 + a(3)^2 + b(3) + c = 27 + 9a + 3b + c = 3$$
Now we have a system of three equations:
$$a + b + c = 0 … (1)$$
$$4a + 2b + c = -6 … (2)$$
$$9a + 3b + c = -24 … (3)$$
Solving this system, we get:
$$a = -3, b = 2, c = 1$$
So,
$$p(x) = x^3 – 3x^2 + 2x + 1$$
Now, we can find \(p(4)\):
$$p(4) = 4^3 – 3(4)^2 + 2(4) + 1 = 64 – 48 + 8 + 1 = 25$$
Therefore final answer is
$$p(4) = 25$$
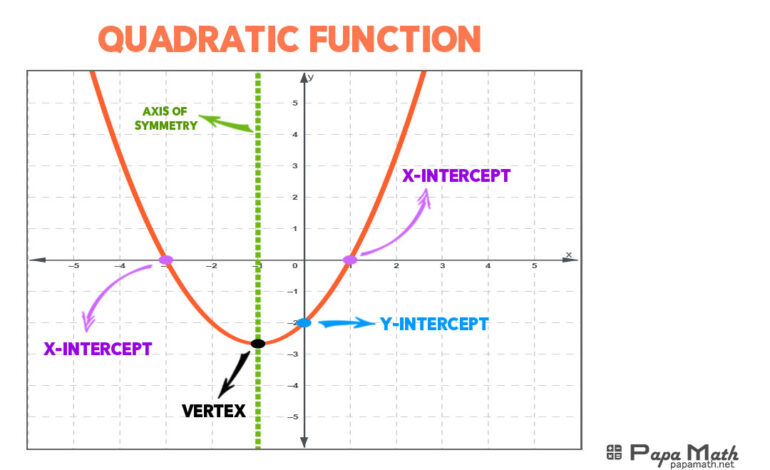
Discover the essence of problem-solving with What is a Quadratic Function?“
FAQs
| Question | Answer |
| Why is it called a cubic function? | It is called a cubic function because its highest degree term is \(x^{3}\) |
| How to solve cubic functions? | Cubic functions are solved by finding the roots using factoring, graphing, or formulas. |
| What is the cubic formula? | The cubic formula is a complex formula used to find the roots of cubic equations. |
| Is a cubic function increasing or decreasing? | A cubic function can be both increasing and decreasing depending on its coefficients. |
| Which is an example of a cubic function? | An example is \(f(x)=x^{3}-4 x^{2}-11 x+30\). |
| Can a cubic function have more than one solution? | Yes, a cubic function can have up to three real solutions. |
Explore the elegant curves and fascinating behaviors of cubic functions through vivid graphs and insightful analysis in Cubic Functions and Their Graphs.
Conclusion
Cubic functions are a fundamental part of algebra and mathematics, with far-reaching applications in various fields. Understanding cubic functions and their graphs is essential for problem-solving, critical thinking, and modeling real-world phenomena. By mastering cubic functions, we can analyze and predict behavior, optimize solutions, and make informed decisions. Whether in physics, engineering, economics, or computer science, cubic functions play a vital role in shaping our understanding of the world. We hope this article has provided valuable insights and inspiration for further exploration of cubic functions and their graphs.
Please feel free to ask your query, and I’ll be happy to answer your query.